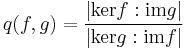Herbrand quotient

In mathematics, the Herbrand quotient is a quotient of orders of cohomology groups of a cyclic group. It was invented by Jacques Herbrand. It has an important application in class field theory.

Contents 1 Definition 1.1 Alternative definition 2 Properties 3 See also 4 References

Definition

If G is a finite cyclic group acting on a G-module A, then the cohomology groups Hⁿ(G,A) have period 2 for n≥1; in other words

Hⁿ(G,A) = Hⁿ⁺²(G,A),

an isomorphism induced by cup product with a generator of H²(G,Z). (If instead we use the Tate cohomology groups then the periodicity extends down to n=0.)

The Herbrand quotient h(G,A) is defined to be the quotient

h(G,A) = |H²(G,A)|/|H¹(G,A)|

of the order of the even and odd cohomology groups, if both are finite.

Alternative definition

The quotient may be defined for a pair of endomorphisms of an Abelian group, f and g, which satisfy the condition fg = gf = 0. Their Herbrand quotient q(f,g) is defined as

if the two indices are finite. If G is a cyclic group with generator γ acting on an Abelian group A, then we recover the previous definition by taking f = 1 - γ and g = 1 + γ + γ² + ... .

Properties

• The Herbrand quotient is multiplicative on short exact sequences. In other words, if

0 → A → B → C → 0

is exact, then

h(G,B) = h(G,A)h(G,C)

• If A is finite then h(G,A) = 1
• If Z is the integers with G acting trivially, then h(G,Z) = |G|
• If A is a finitely generated G-module, then the Herbrand quotient h(A) depends only on the complex G-module C⊗A (and so can be read off from the character of this complex representation of G).

These properties mean that the Herbrand quotient is usually relatively easy to calculate, and is often much easier to calculate than the orders of either of the individual cohomology groups.

See also

• Class formation

References

• M. F. Atiyah and C. T. C. Wall, "Cohomology of Groups", in Algebraic Number Theory by J. W. S. Cassels, A. Frohlich ISBN 0-12-163251-2, Chapter IV. See section 8.
• Emil Artin, John Torrence Tate, Class Field Theory (AMS Chelsea, 2008) ISBN 0821844261, page 5.
• Gerald J. Janusz, Algebraic number fields. Pure and Applied Mathematics 55 (Academic Press, 1973) page 142.